Now that we know how to play a single note with Commodore 64 BASIC, why not make something more complex? On this post, we’ll play simple melodies using one SID voice. Again, that’s not that exciting, but those simple things are necessary in order to go deeper on SID music programming on a later time.
Sample programs are both available on the Commodore 64 user’s manual and on the Commodore 64 Programmer’s Reference Guide. But, those examples all make use of numbers to represent notes. Instead of putting the frequencies onto DATA statements, we are now going to represent musical notes using the international notation.
So, we have seven natural notes:
C, D, E, F, G, A, B
and five sharp notes:
C#, D#, F#, G#, A#
On our program, we will use a string to hold the information about the note to play. The first character of the string is the note, the second character may be a space (natural note) or a sharp (sharp note). Finally, the third character is the octave the note belongs to.
Then, we will use an integer value for the duration of the note.
All of this information will be put on DATA lines. So, in order to play the notes C3 and D#3 with a duration of 1/4, we will use the following DATA line:
DATA C 3, 4, D#3, 4
Please note that on some situations quotes are not mandatory on strings in DATA lines. This is the case, for instance, if control characters or punctuation characters are not used. This way, notes entering will be easier.
Talking about note frequencies, the frequency of a note will be evaluated starting from A0 (the A note on the first octave). Half-tones will be added to A0, then the resulting note will be transposed on the required octave. This is done as follows:
fs=int((466*a^n)*2^OC)
So, the frequency of a note is computed starting from the SID frequency value of A0, which is 466. a is a constant (we know it from this article), n is the number of half-tones past A0, and OC is the octave.
The program associates the right number of half-tones to each note. So, C is 0 half-tones past C0, C# is one half-tone past C0, D is two half-tones past C0 and so on.
DOWNLOAD: playing one voice tunes with C64 BASIC V2
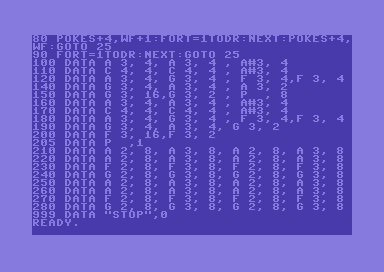
Some explanations of the program are in order.
On line 5, some powers are pre-computed so that evaluating the term \( 2^{OC} \) in the frequency formula is faster.
On line 25, music data is read (a string with note, octave and sharp sign and a number with note duration).
On line 30, note name, octave and sharp sign are extracted. Please note that the sharp sign may be missing (this is the case when dealing with natural notes). Then, the number of half-tones is computed (starting with the ASCII code of the note’s name).
Line 35 handles a pause.
Lines 36 and 37 make an adjustment due to the fact that between E and F there’s only one half-tone. So, the number of half-tones from the reference note is reduced by one.
On lines 38 and 39, numbers of half-tones for notes A and B are directly assigned. This is due to the fact that while notes from C to G are in alphabetical order, notes A and B are not.
Line 40 adds one half-tone for sharp notes.
Lines 50, 55 and 60 compute SID frequencies, split them in low byte and high byte, then poke these values on SID frequency registers.
Line 65 computes the note’s duration. The duration is a fraction of the value TM, assigned on line 12. So, it is possible to change the speed of the tunes by just changing the value of TM.
As a final note, if you are willing to enter your own melodies on the program, please note that note durations may need some adjustment, as BASIC is not that fast.
Ciao Marcello! Ottimo articolo!