On my last post I had presented an 8 bit fast multiply routine. Actually, it was limited to a narrower range of numbers, as it was custom designed for a certain program. Now, we are going to present a general 8 bit fast multiply routine.
; fast multiply 8 bit
multiply_ab_fast
lda #>square_low
sta mod1+2
lda #>square_high
sta mod2+2
clc
lda multiplicand
adc multiplier
bcc skip_inc
inc mod1+2
inc mod2+2
skip_inc tax
sec
lda multiplicand
sbc multiplier
bcs no_diff_fix
sec
lda multiplier
sbc multiplicand
no_diff_fix
tay
sec
mod1 lda square_low,x
sbc square_low,y
sta result+1
mod2 lda square_high, x
sbc square_high, y
sta result
rts
This routine accepts 8 bit numbers in the full range 0…255 (the previous routine was only capable of multiplying numbers in the range 0…127 for one factor, 0…90 for the other one).
This time, square tables must be 16 bit. Thus, the code has been modified so that 16 bit indexing is made possible. This is only required when looking for the term ((a+b)^2)/4, as the unsigned difference |a-b| will always remain in the 8 bit range.
To look for the term ((a+b)^2)/4, the sum a+b is used as an index, ranging from 0 to 510. That sums up to 511 different values. The x index is used along with self-modifying code to reach this range.
I have tested this routine with a BASIC program and with some assembly language programs and it seems to work fine.
The following Commodore 64 code can be assembled with DASM. Decimal addresses of parameters used are available in the comments, so that it is possible to test this routine. The code also includes the tables of squares (a 1022 bytes table is needed here).
DOWNLOAD: fast 8 bit multiply (source code)
DOWNLOAD: fast 8 bit multiply (prg file)

Performing a 16 bit multiply using an 8 bit multiply routine
Extending the above routine to the 16 bit range is not that easy, as a huge table would be required, eating up all of the memory available. But, we can use the above routine as a part of a 16 bit multiply routine, without the need of any bit-shifting instruction (ASL, ROL, etc.). The result will not be a fast 16 bit routine, but it’s just something that feels quite unusual. However, this 16 bit routine can be adjusted on particular situations, maybe offering better performances than a standard bit-shifting 16 bit multiply routine.
The principle
Given two 16 bit numbers A and B, it is possible to write them by using their high bytes and low bytes:
A = AH * 256 + AL B = BH * 256 + BL with: AH = INT(A/256) AL = A-256*AH BH = INT(B/256) BL = B-256*BH
Using those expressions, the product A * B can be written as:
A * B = (AH * 256 + AL) * (BH * 256 + BL)
It can be shown that the above equation can be rewritten as:
A * B = 65536*(AH*BH)+256(AH*BL+AL*BH)+AL*BL
So, the product of the two 16 bit numbers A and B can be written as a linear combination of four products, with factors made up of the low bytes and the high bytes of the original 16 bit factors.
This seems to be pretty useless for practical applications. But, this approach does make it possible to use the above 8 bit routine for 16 bit multiplications.
A large number like 65536 seems intimidating, but no multiplication is actually required. Multiplying by 65536 is obtained by two byte shifts. That means, we can multiply by 65536 by just re-arranging the bytes of the number to be multiplied. Likewise, multiplying by 256 it’s just a one byte shift. So, no slow bit-shifting instructions are really required to perform the above multiplications by constants. Those constants are just powers of two, that’s why life is getting so easier here.
The code
The following code hopefully demonstrates the above approach. The generic 16 bit routine seems to reach the very same speed of a classic 16 bit multiply routine – with a much longer code, so that’s not a deal. Still, a few testing code can improve its efficiency.
For instance, if we happen to multiply two 8 bit numbers, we can avoid the product 65536*(AH*BH) by testing for zero the high bytes of the 16 bit factors.
Furthermore, if either BL or AL are 0, the product 256*(AH*BL+AL*BH) can be computed faster, as it is possible to avoid at least one call to the 8 bit multiply routine.
Finally, if we only need the two lower bytes of the result (that is, we only need a 16 bit multiplication with 16 bit result), the term 65536*(AH*BH) can be simply ignored.
Source code (16 bit multiply using 8 bit multiply routine)
Source code (16 bit multiply with 8 bit routine, optimized, zero check version)
The following screenshots show a couple of tests. A simple BASIC program can be written, so that tests are faster and easier.
The following programs (we already know them) have been modified to include the above routines.
DOWNLOAD: drawing lines with 16/8 multiply routine (source code)
DOWNLOAD: drawing lines with 16/8 multiply routine (prg file)
DOWNLOAD: Mandelbrot set program with 16/8 multiply (source code)
DOWNLOAD: Mandelbrot set program with 16/8 multiply (prg file)
The fractal program actually makes use of an optimized version, taking into account the fact that the two higher bytes of the 16 bit product are not needed. In this particular case, we actually get a fast 16 bit multiply routine outperforming its classic 16 bit bit-shifting counterpart. The fact that most of the time the factors are actually limited to the 8 bit range also helps.
Instead, in the drawing lines program, we get the very same performance as a standard bit-shifting multiply routine.
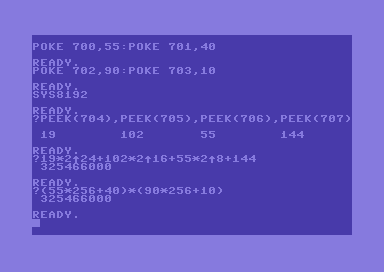
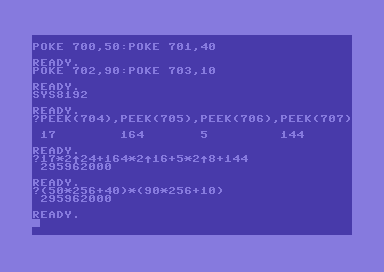
Tip, you don’t need that fixup if you adjust the tables.
Also see my entry at codebase – 16bit mult can take 200 cycles
https://codebase64.org/doku.php?id=base:6502_6510_maths
Hi! Thank you so much!