Again on random numbers. This time, we’ll have a look at how to generate fractals by using random numbers. It may seem strange, as random numbers don’t have a rule. They just are wild, and if you use them to draw points, those will pop up everywhere without any kind of rule.
This wild behaviour of random numbers is know as chaos. At least, this is a rough idea of the concept.
But how can we draw fractals by using random numbers? Fractals have a rule, have an order in their points, they mostly have self similarity… In a way we are pretending that totally screwed-up guys would design something perfect. But hey, sometimes that happens in life!
And so yes, we can make order out of disorder. We can draw a fractal out of random numbers. But still, all of this doesn’t come from complete magic. In fact, we need at least a rule on how to “chose” those random numbers.
Stage 1: creating a random point inside a triangle
Imagine you have a triangle. The first thing to learn is drawing random points inside it. As I never did such a thing, it was a bit difficult for me to figure out the required piece of code.
The point is not just figuring out a properly working code… but something reasonably fast for BASIC. So, forget things like: we create a random point, we draw lines connecting that point to the vertexes of the triangle, then we check if any of those lines intersect with the triangle… not what we need.
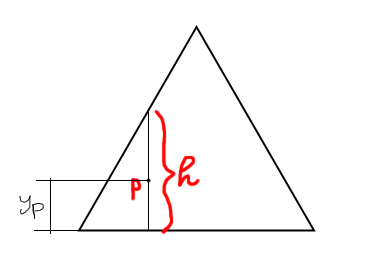
A faster way is this. First of all, take the x-coordinate of the random point. Then, check if y-coordinate of the random point is less than the length h (see picture).
If that is the case, the point is inside the triangle. If not, it is outside and must be discarded.
Things will stop working when x-coordinate of the random point goes past the left half of the triangle (imagine the x-coordinate of P going to the right). But, we can do a mirroring of the x-coordinate and think that we are still on the first half of the triangle. This way things will work just nicely. Just imagine having two right triangles and doing the check on both. This is the idea.
But how do we compute h? From simple trigonometry we can say: h = xP / tan (pi/6). So, if we know the x-coordinate of the random point (and we do know), we can calculate h with ease. And a random point will be inside the triangle if its y-coordinate is less than h.
h can be seen as the height of a small right triangle inside the main triangle. So finding h is just a simple matter of triangle trigonometry, as shown.
Those are the main concepts you’ll find in the code. Some minor adjustments have been done since on the bitmap screen the origin is on the top left-corner of the video. Instead, in math we put the origin on the bottom left-corner of the video (we look at it like a quadrant).
There’s chaos but there’s also a rule
Ok, we can now draw a random point inside the triangle. So what are we going to do with it? Just imagine to connect this point to a random vertex of the triangle. Then, take the middle point of this segment. That’s it – the middle point is another point of the fractal. Now, take this last point and connect it to a random vertex of the triangle. Again, take the middle point of this segment… and repeat again and again.
Although any vertex is chosen totally randomly, what you’ll get is something that looks very close to a Sierpinsky triangle fractal:
Will the same work on a square? Yes, but you have to modify the code so that the same random vertex cannot be chosen twice in a sequence. And on a square, the checks for inner points are much easier. Here’s the result:
The programs
Here are the two BASIC programs drawing the fractals. Those are all but fast. So, better to run them with warp mode on emulators or with some kind of accelerator on a real machine. Still, it’s a matter of waiting some minutes, not hours. An assembly implementation would be quite the right thing, but I am lacking time for it nowadays.
The code is something old, something new. The bitmap handling routines are just the BASIC versions of my previous assembly line-drawing routines. I tried to optimize this part of the program the best that I could. You have to wait at the beginning for creating plotting tables, but the speed improvement while plotting points on screen pays for that initial wait I hope.
There are two programs in the directory, each drawing a single fractal. Let’s have a look at the code of the fractal with triangles.
A brief tour on the code
The subroutine from line 240 is the one responsible for creating a random point. After creating it, it sets the flag PF to 0 or 1, according to whether the point is inside the triangle or not. This way, the main program can call the routine again if needed, until a point inside the triangle will be found.
Line 240 just creates the random coordinates of points (XR and YR).
Line 242 checks if x-coordinate of the random point is out of range. If so, it adjusts XR coordinate so that it is between the width of the triangle.
Line 244 creates a variable XK. This is needed, because if we need mirroring XR, we must not loose the original value of XR. The mirroring takes place when XR is greater than 160, as we are in the right-half of the triangle. If we didn’t do so, the computed value YC on the following line would have no meaning.
Line 246 computes YC using trigonometry.
Line 248 sets the flag for inner point according to results.
Lines from 325 to 360 actually draw the fractal.
Subroutine from line 240 is called. After this, result is checked. If the random point generated is inside the triangle, program flow goes to the next line. Otherwise, subroutine 240 is called again, until a point inside the triangle is found.
Vertices coordinates are now stored on a real array. At this point, a random index to pick up an array element is generated, so that a random vertex can be selected.
Finally, the middle point between the random point and the vertex is calculated and plotted. The program then jumps back again to line 340, plotting more and more points of the fractal.
References
“Chaos Game – Fractals emerging from chaos – Computer simulation” by Think Twice.


Too Cool! Thank you. I passed Finite Math in College because my professor had an obsession with Fractals and the Mandlebrot Set. I really was terrible at math, but even in the late 80s/early 90s had an ability to find things for him. And, for that – I passed Finite. The story of Benoit Mandlebrot is pretty interesting too. And, to know – a creator obviously had a hand in everything in nature as evidenced by the mathematical nature found there.