Estimating PI using Monte Carlo Method (C64, BASIC)

OK, it’s not PI day, but I wanted to have a trial at estimating PI using Monte Carlo Method anyway.

Many methods use some mathematical “trick” to get an approximate value of PI. For instance, you can use limits, series and so on. But, estimating PI using Monte Carlo Method is something quite different.

With Monte Carlo Method, you are not creating a succession of values that eventually converge to an approximate value of PI. Rather, by using random numbers you create a succession of numbers that eventually will hopefully stabilize on an approximate value of PI.

With other methods you can get a succession of approximation values. And the newest value is always closer to PI than the oldest. This is not the case with the Monte Carlo method. This is kind of reasonable after all, since with this method we are using random number.

A square and a circle

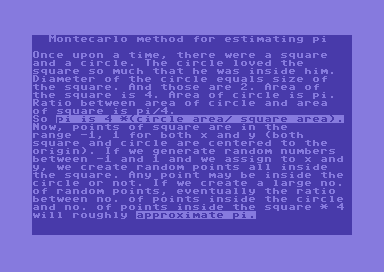
Imagine a square with a size of 2. And imagine a circle inside the square with a diameter again of 2. Both are centered to the origin.

The area of such a square is 4. And the area of such a circle is PI (the area of a circle is PI * R^2).

Now, the ratio between the area of the circle and the area of the square is, of course, PI/4.

Now that’s the idea! If we get a way to estimate that ratio, then we get an estimation of PI as well!

And here we go to Monte Carlo

Have you ever been on a Casino? Me not… But still, we are now going to deal with random numbers. Hope we will be lucky…

Now, a square of size 2, centered to the origin, is made up of (X, Y) points with their coordinates all belonging to the range [-1, +1].

Here’s what random numbers are all about in here. If we create many random numbers in the range [-1, 1], of course all points will belong to the size 2 square. As for the circle instead, some points will belong to it, others will not.

So the idea is that if we generate a huge quantity of random points, the points inside the circle will give an estimate of the area of the circle itself. And similarly, the total number of random points created will give an estimate of the area of the square (remember that the total number of points created belong to the square for sure).

So, if we compute the ratio number points inside circle/ total number of points it’s very likely that we will get an estimate of PI!

The programs

The first program is quite straight and uses random numbers with as many decimal digits as the RND() function offers.

The second program makes use of offsets to increase the precision of numbers. This is some sort of mixing between floating point math and integer math.  This approach allows – for a very huge quantity of random numbers created – a better estimate of PI.

Download: Pi with Monte Carlo

Programs are both quite slow and need to be run at least for a hour or so on the real machine (warp mode really helps if using an emulator). Collectors may have a Super CPU, that helps as well (lucky you!).

With the first program (“montecarlo v3”), using random numbers with 9 decimal digits, we get eventually an approximation of roughly 3.146. Instead, with the second program (“mont.digits”), we get an approximation of roughly 3.141.

As PI is roughly 3.14159, the second program, though slower, gives a better approximation.

The more you let the programs run, the more the computed ratio will tend to stabilize to a certain approximation of PI.

A note is also included in the .d64 image for a quick review of the principle.

We cannot talk about a converging process, as we are dealing with random numbers. Still, it’s quite impressing that with this method we can get a reasonable approximation of PI, isn’t it? Statistics seems to work quite well here.